Алгоритм D*

Алгоритм D*(Дейкстры)-позволяет нам задавать приоритеты исследования путей. Вместо равномерного исследования всех возможных путей, он отдает предпочтение путям с наиболее низкой "стоимостью".

Создавая, проекты, связанные с перемещением, программируемого объекта, мы часто сталкиваемся с проблемой поиска кратчайшего пути из одной точки в другую. В этой статье мы подробно рассмотрим Алгоритм поиска кратчайшего пути известного как Алгоритм D* так же известный, как Алгоритм Дейкстры.

Для начала попробуем разобраться в принципе работы алгоритма:

Ошибка создания миниатюры: Файл не найден

Обратим свое внимании на представленный граф. Предположим, что вершины на нем-это населенные пункты, а ребра-это дороги с указанной стоимостью проезда. Как становится понятно, нам необходимо добраться из одной точки в другую за минимальную стоимость. Т. е. найти наиболее оптимальный путь из А в В.

Здесь нам понадобится структура данных, известная как "Куча", которая будет реализовывать приоритетную очередь.

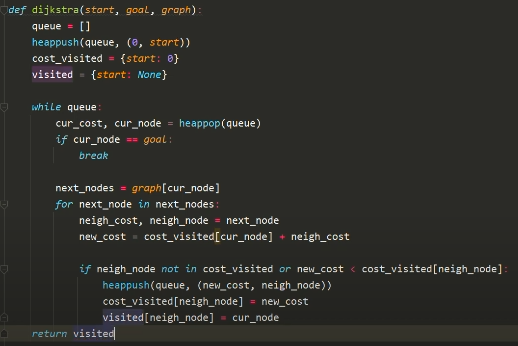
Напишем алгоритм на языке Python.

Сам граф будет состоять из списка смежностей, в которых элементы теперь являются картежами, где на первом месте указана стоимость проезда к вершине, на втором сама вершина.

И так, в алгоритме D* на ряду с приоритетной очередью, мы создадим словарь, чтобы следить за общей стоимостью движения с начальной вершины, а в цикле будем вынимать вершину из очереди с минимальной ценой, затем для всех смежных вершин будем рассчитывать новую цену перемещения от текущей вершины, и если новой вершины не окажется в словаре стоимости пути до нее или новая цена будет ниже, чем уже имеется, то занесем эту вершину в очередь и обновим стоимость пути до нее, и запишем, что пришли к этой вершине из текущей.

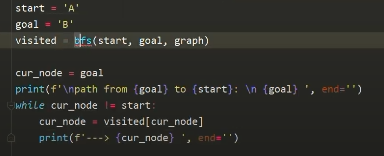
не забываем добавить восстановление пути:

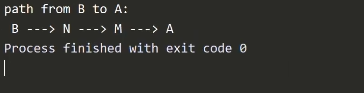
Применив алгоритм, мы видим самый "дешевый" путь в нашем графе: