Алгоритм D*: различия между версиями
Sonya (обсуждение | вклад) Нет описания правки |
Sonya (обсуждение | вклад) Нет описания правки |
||
| Строка 1: | Строка 1: | ||
Алгоритм D*(Дейкстры)-позволяет нам задавать приоритеты исследования путей. Вместо равномерного исследования всех возможных путей, он отдает предпочтение путям с наиболее низкой "стоимостью". | '''Алгоритм D*(Дейкстры)'''-позволяет нам задавать приоритеты исследования путей. Вместо равномерного исследования всех возможных путей, он отдает предпочтение путям с наиболее низкой "стоимостью". | ||
Создавая, проекты, связанные с перемещением, программируемого объекта, мы часто сталкиваемся с проблемой поиска кратчайшего пути из одной точки в другую. В этой статье мы подробно рассмотрим Алгоритм поиска кратчайшего пути известного как Алгоритм D* так же известный, как Алгоритм Дейкстры. | Создавая, проекты, связанные с перемещением, программируемого объекта, мы часто сталкиваемся с проблемой поиска кратчайшего пути из одной точки в другую. В этой статье мы подробно рассмотрим Алгоритм поиска кратчайшего пути известного как Алгоритм D* так же известный, как Алгоритм Дейкстры. | ||
| Строка 41: | Строка 41: | ||
не забываем добавить восстановление пути: | не забываем добавить восстановление пути: | ||
<syntaxhighlight lang="c"> | |||
start = 'A' | |||
goal = 'B' | |||
visited = bfs(start, goal, graph) | |||
cur_node = goal | |||
print(f'\npath from {goal} to {start}: \n {goal} ', end=' ') | |||
while cur_node |= start: | |||
cur_node = visited [cur_node] | |||
print(f'--->{cur_node} ', end=' ') | |||
</syntaxhighlight> | |||
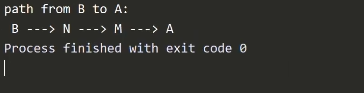
Применив алгоритм, мы видим самый "дешевый" путь в нашем графе: | Применив алгоритм, мы видим самый "дешевый" путь в нашем графе: | ||
[[Файл:D*code3.png|безрамки|364x364пкс|альт=|центр]] | [[Файл:D*code3.png|безрамки|364x364пкс|альт=|центр]] | ||
Текущая версия от 16:31, 7 июня 2021
Алгоритм D*(Дейкстры)-позволяет нам задавать приоритеты исследования путей. Вместо равномерного исследования всех возможных путей, он отдает предпочтение путям с наиболее низкой "стоимостью".
Создавая, проекты, связанные с перемещением, программируемого объекта, мы часто сталкиваемся с проблемой поиска кратчайшего пути из одной точки в другую. В этой статье мы подробно рассмотрим Алгоритм поиска кратчайшего пути известного как Алгоритм D* так же известный, как Алгоритм Дейкстры.
Для начала попробуем разобраться в принципе работы алгоритма:
Обратим свое внимании на представленный граф. Предположим, что вершины на нем-это населенные пункты, а ребра-это дороги с указанной стоимостью проезда. Как становится понятно, нам необходимо добраться из одной точки в другую за минимальную стоимость. Т. е. найти наиболее оптимальный путь из А в В.
Здесь нам понадобится структура данных, известная как "Куча", которая будет реализовывать приоритетную очередь.
Напишем алгоритм на языке Python.
Сам граф будет состоять из списка смежностей, в которых элементы теперь являются картежами, где на первом месте указана стоимость проезда к вершине, на втором сама вершина.
И так, в алгоритме D* на ряду с приоритетной очередью, мы создадим словарь, чтобы следить за общей стоимостью движения с начальной вершины, а в цикле будем вынимать вершину из очереди с минимальной ценой, затем для всех смежных вершин будем рассчитывать новую цену перемещения от текущей вершины, и если новой вершины не окажется в словаре стоимости пути до нее или новая цена будет ниже, чем уже имеется, то занесем эту вершину в очередь и обновим стоимость пути до нее, и запишем, что пришли к этой вершине из текущей.
def dijkstra(start, goal, graph):
queue = []
heappush(queue, (0, start))
cost_visited = {start: None}
visited = {start: None}
while queue:
cur_cost, cur_node = heappop(queue)
if cur_node == qoal:
break
next_nodes = graph[cur_node]
for next_node in next_nodes:
neigh_cost, neigh_node = next_node
new_cost = cost_visited[cur_node] + neigh_cost
if neigh_node not in cost_visited or new_cost < cost_visited[neigh_node]:
heappush(queue, (new_cost, neigh_node))
cost_visited[neigh_mode] = new_cost
visited[neigh_node] = cur_node
return visited
не забываем добавить восстановление пути:
start = 'A'
goal = 'B'
visited = bfs(start, goal, graph)
cur_node = goal
print(f'\npath from {goal} to {start}: \n {goal} ', end=' ')
while cur_node |= start:
cur_node = visited [cur_node]
print(f'--->{cur_node} ', end=' ')
Применив алгоритм, мы видим самый "дешевый" путь в нашем графе: